Minimum action method to predict nonequilibrium phase transitions
First-order nonequilibrium phase transitions observed in active matter, fluid dynamics, biology, climate science, and other systems with irreversible dynamics are challenging to analyze because they cannot be inferred from a simple free energy minimization principle. Relying on the dynamics is crucial to understand how the system may go from one metastable state to the other. It turns out that the theory of large deviation brings an answer to this question. By minimizing an action that plays the role of a free energy in the space of all possible paths, one can find the most probable realisation of the noise that drives the system out of a basin of attraction. This also yields the preferred state of the system when comparing escape probabilities. Below are displayed two movies showing how a minimum action algorithm finds optimal escape paths joining two fixed points. The path with highest action has a larger ''cost of noise'' and thus indicates that the associated transition is less probable than the reverse one. The first-order transition occurs when the escape paths in both directions have the same minimum actions.
Field-mediated interactions between active particles
Systems of independent active particles embedded into a fluctuating environment are relevant to many areas of soft-matter science. Transmembrane proteins such as ATP-binding cassette transporters, or Kcsa potassium channels enter this class of active particles since these transmembrane gates can usually be found in two states, closed or opened, depending on chemical environment, and their conformation change locally shapes the cell membrane. We can build a minimal model of spin-carrying Brownian particles in a Gaussian field and show that activity-driven spin dynamics can lead to patterned order. We find that the competition between field-mediated interactions and active noise alone can yield such diverse behaviors as phase transitions and microphase separation, from lamellar up to hexagonal ordering of clusters of opposite magnetization. We find regimes of stationary patterns, but also dynamical regimes of relentless birth and growth of lumps of magnetization opposite of the surrounding one. Our approach combines Monte Carlo simulations with analytical methods based on dynamical density functional approaches.
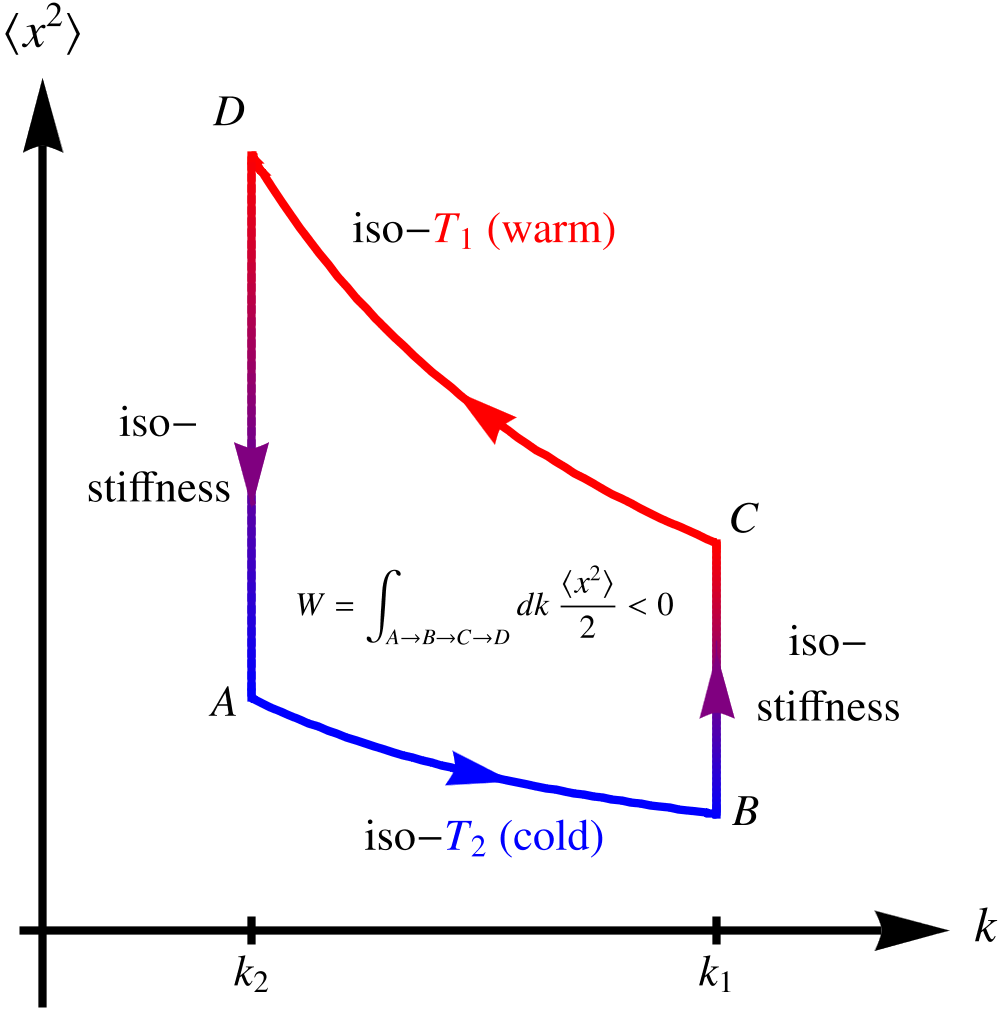
Stochastic Stirling Engine
A Stirling engine made of a colloidal particle in contact with a nonequilibrium bath is considered and analyzed with the tools of stochastic energetics. We model the bath by non Gaussian persistent noise acting on the colloidal particle. Depending on the chosen definition of an isothermal transformation in this nonequilibrium setting, we find that either the energetics of the engine parallels that of its equilibrium counterpart or, in the simplest case, that it ends up being less efficient. Persistence, more than non-Gaussian effects, are responsible for this result.